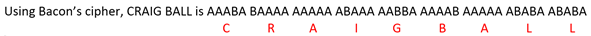Where does the average person encounter binary data? Though we daily confront a deluge of digital information, it’s all slickly packaged to spare us the bare binary bones of modern information technology. All, that is, save the humble Universal Product Code, the bar code symbology on every packaged product we purchase from a 70-inch TV to a box of Pop Tarts. Bar codes and their smarter Japanese cousins, QR Codes, are perhaps the most unvarnished example of binary encoding in our lives.
Barcodes have an ancient tie to e-discovery as they were once used to Bates label hard copy documents, linking them to “objective coding” databases. A lawyer using barcoded documents was pretty hot stuff back in the day.
Just a dozen numeric characters are encoded by the ninety-five stripes of a UPC-A barcode, but those digits are encoded so ingeniously as to make them error resistant and virtually tamperproof. The black and white stripes of a UPC are the ones and zeroes of binary encoding. Each number is encoded as seven bars and spaces (12×7=84 bars and spaces) and an additional eleven bars and spaces denote start, middle and end of the UPC. The start and end markers are each encoded as bar-space-bar and the middle is always space-bar-space-bar-space. Numbers in a bar code are encoded by the width of the bar or space, from one to four units.

The bottle of Great Value purified water beside me sports the bar code at right.
Humans can read the numbers along the bottom, but the checkout scanner cannot; the scanner reads the bars. Before we delve into what the numbers signify in the transaction, let’s probe how the barcode embodies the numbers. Here, I describe a bar code format called UPC-A. It’s a one-dimensional code because it’s read across. Other bar codes (e.g., QR codes) are two-dimensional codes and store more information because they use a matrix that’s read side-to-side and top-to-bottom.
The first two black bars on each end of the barcode signal the start and end of the sequence (bar-space-bar). They also serve to establish the baseline width of a single bar to serve as a touchstone for measurement. Bar codes must be scalable for different packaging, so the ability to change the size of the codes hinges on the ability to establish the scale of a single bar before reading the code.
Each of the ten decimal digits of the UPC are encoded using seven “bar width” units per the schema in the table at right.
To convey the decimal string 078742, the encoded sequence is 3211 1312 1213 1312 1132 2122 where each number in the encoding is the width of the bars or spaces. So, for the leading value “zero,” the number is encoded as seven consecutive units divided into bars of varying widths: a bar three units wide, then (denoted by the change in color from white to black or vice-versa), a bar two units wide, then one then one. Do you see it? Once more, left-to-right, a white band, three units wide, a dark band two units wide , then a single white band and a single dark band (3-2-1-1 encoding the decimal value zero).
You could recast the encoding in ones and zeroes, where a black bar is a one and a white bar a zero. If you did, the first digit would be 0001101, the number seven would be 0111011 and so on; but there’s no need for that, because the bands of light and dark are far easier to read with a beam of light than a string of printed characters.
Taking a closer look at the first six digits of my water bottle’s UPC, I’ve superimposed the widths and corresponding decimal value for each group of seven units. The top is my idealized representation of the encoding and the bottom is taken from a photograph of the label:
Now that you know how the bars encode the numbers, let’s turn to what the twelve digits mean. The first six digits generally denote the product manufacturer. 078742 is Walmart. 038000 is assigned to Kellogg’s. Apple is 885909 and Starbucks is 099555. The first digit can define the operation of the code. For example, when the first digit is a 5, it signifies a coupon and ties the coupon to the purchase required for its use. If the first digit is a 2, then the item is something sold by weight, like meats, fruit or vegetables, and the last six digits reflect the weight or price per pound. If the first digit is a 3, the item is a pharmaceutical.
Following the leftmost six-digit manufacturer code is the middle marker (1111, as space-bar-space-bar-space) followed by five digits identifying the product. Every size, color and combo demands a unique identifier to obtain accurate pricing and an up-to-date inventory.
The last digit in the UPC serves as an error-correcting check digit to ensure the code has been read correctly. The check digit derives from a calculation performed on the other digits, such that if any digit is altered the check digit won’t match the changed sequence. Forget about altering a UPC with a black marker: the change wouldn’t work out to the same check digit, so the scanner will reject it.
In case you’re wondering, the first product to be scanned at a checkout counter using a bar code was a fifty stick pack of Juicy Fruit gum in Troy, Ohio on June 26, 1974. It rang up for sixty-seven cents. Today, 45 sticks will set you back $2.48 (UPC 22000109989).